The Power of Deep Q-Networks (DQN) in Reinforcement Learning

DQN became famous in 2015 when DeepMind used it to achieve human-level performance in playing Atari games. This breakthrough demonstrated DQN’s power to handle problems that were previously too challenging for conventional RL methods.

A Deep Q-Network (DQN) is an extension of Q-Learning that uses a neural network to estimate Q-values instead of relying on a large Q-Table. In traditional Q-Learning, the Q-Table stores values for every state-action pair, which quickly becomes impractical for environments with large or continuous state spaces. DQN addresses this by using a neural network to approximate these Q-values.

Why is DQN Powerful?

• Handles Complex, High-Dimensional State Spaces: DQN can manage inputs like images or sensor data without requiring discretization, making it suitable for tasks like video game playing or robotics.
• Efficient Learning: By using a neural network, DQN generalizes across similar states, allowing the agent to learn more effectively.

In simple terms, DQN is like giving our agent a brain that can understand and adapt to complex environments by finding patterns in the data it receives.

DQN follows a process similar to Q-Learning but incorporates two key enhancements that make it much more effective:

1. Experience Replay: Instead of learning from each experience in the order it occurs, the agent stores past experiences in a replay buffer. During training, it samples a random batch of experiences from this buffer, which helps break the correlation between consecutive experiences. This technique stabilizes learning and improves sample efficiency, allowing the agent to learn more effectively from fewer interactions with the environment.
2. Target Network: DQN maintains two separate neural networks — a policy network that predicts Q-values and a target network that calculates target Q-values. The target network is updated periodically with the weights of the policy network, helping prevent the training process from becoming unstable.

In Q-Learning, the Q-value update is performed using a formula where DQN modifies this by using a neural network to approximate Q-values. Instead of directly updating a Q-Table, DQN adjusts the weights of the neural network to minimize the difference between the predicted Q-value and the target Q-value.

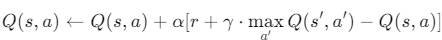
The neural network is trained to minimize the difference between the predicted Q-value and this target value using gradient descent, which gradually improves its accuracy.

Imagine you’re playing a platformer video game where your goal is to collect coins while avoiding enemies. At first, you randomly move around — sometimes finding coins, sometimes hitting enemies. Over time, you start recognizing patterns: moving left might lead to a coin, while jumping over a specific obstacle helps avoid danger.

In DQN, the neural network functions like your brain, learning from these experiences and gradually improving its understanding of which actions lead to rewards or penalties. Unlike Q-Learning, which would need to remember every possible move, DQN generalizes. If two situations are similar, DQN can apply what it learned from one to the other, allowing it to learn much faster.

Why Use Experience Replay and Target Networks?

Think of experience replay as keeping a journal of all your past moves. Instead of learning from just the most recent action, you revisit past experiences to understand what worked and what didn’t, making your learning process much more robust. The target network, on the other hand, acts like a mentor who doesn’t change opinions too often, helping you stay on track with your learning.

Step 1: Setting Up the Environment and Neural Network

    
        import gymnasium as gym
        import torch
        import torch.nn as nn
        import torch.optim as optim
        import random
        import numpy as np
        from collections import deque

        # Create the environment
        env = gym.make('CartPole-v1')

        # Define the neural network
        class DQN(nn.Module):
            def __init__(self, input_size, output_size):
                super(DQN, self).__init__()
                self.fc1 = nn.Linear(input_size, 24)
                self.fc2 = nn.Linear(24, 24)
                self.fc3 = nn.Linear(24, output_size)

            def forward(self, x):
                x = torch.relu(self.fc1(x))
                x = torch.relu(self.fc2(x))
                return self.fc3(x)

        # Initialize networks
        input_size = env.observation_space.shape[0]  # 4 inputs: position, velocity, angle, angular velocity
        output_size = env.action_space.n  # 2 outputs: left or right
        policy_net = DQN(input_size, output_size)
        target_net = DQN(input_size, output_size)
        target_net.load_state_dict(policy_net.state_dict())  # Copy weights from policy network to target network
        target_net.eval()

        # Optimizer and loss function
        optimizer = optim.Adam(policy_net.parameters())
        loss_fn = nn.MSELoss()
    

The neural network approximates the Q-values, with 4 input features (state of the cart) and 2 output actions (left or right). We have two networks: the policy network for predicting actions and the target network for calculating the target Q-values.

Step 2: Experience Replay

    
        # Replay buffer
        replay_buffer = deque(maxlen=5000)

        # Function to store experience in replay buffer
        def store_experience(state, action, reward, next_state, done):
            replay_buffer.append((state, action, reward, next_state, done))

        # Sample a batch of experiences from the buffer
        def sample_experiences(batch_size):
            return random.sample(replay_buffer, batch_size)
    

The replay buffer allows the agent to learn from past experiences, helping stabilize training.

Step 3: Training the DQN

    
        # Training parameters
        batch_size = 64
        gamma = 0.99
        epsilon = 1.0
        epsilon_min = 0.01
        epsilon_decay = 0.995
        target_update_frequency = 100
        episodes = 5000

        for episode in range(episodes):
            state = env.reset()[0]
            done = False
            total_reward = 0

            while not done:
                # Epsilon-greedy action selection
                if random.uniform(0, 1) < epsilon:
                    action = env.action_space.sample()  # Explore
                else:
                    action = np.argmax(policy_net(torch.FloatTensor(state)).detach().numpy())  # Exploit

                next_state, reward, done, _, _ = env.step(action)
                total_reward += reward

                store_experience(state, action, reward, next_state, done)
                state = next_state

                # Train the network if the buffer has enough experiences
                if len(replay_buffer) > batch_size:
                    experiences = sample_experiences(batch_size)
                    states, actions, rewards, next_states, dones = zip(*experiences)

                    # Convert to PyTorch tensors
                    states = torch.FloatTensor(states)
                    actions = torch.LongTensor(actions)
                    rewards = torch.FloatTensor(rewards)
                    next_states = torch.FloatTensor(next_states)
                    dones = torch.FloatTensor(dones)

                    # Calculate Q-values
                    current_q_values = policy_net(states).gather(1, actions.unsqueeze(1)).squeeze(1)
                    next_q_values = target_net(next_states).max(1)[0]
                    target_q_values = rewards + gamma * next_q_values * (1 - dones)

                    loss = loss_fn(current_q_values, target_q_values.detach())
                    optimizer.zero_grad()
                    loss.backward()
                    optimizer.step()

                if epsilon > epsilon_min:
                    epsilon *= epsilon_decay

                if episode % target_update_frequency == 0:
                    target_net.load_state_dict(policy_net.state_dict())

                if episode % 100 == 0:
                    print(f"Episode {episode + 1}: Total Reward: {total_reward}")

        env.close()
    

We use the epsilon-greedy strategy to balance exploration and exploitation. The target network is updated periodically to stabilize training.

Step 4: Testing the DQN Agent

    
        env = gym.make('CartPole-v1', render_mode="human")

        def test_dqn_agent(episodes=1):
            for episode in range(episodes):
                state = env.reset()[0]
                done = False
                steps = 0

                while not done:
                    env.render()
                    action = np.argmax(policy_net(torch.FloatTensor(state)).detach().numpy())
                    state, _, done, _, _ = env.step(action)
                    steps += 1

                print(f"Test Episode {episode + 1}: Balanced for {steps} steps.")
                env.close()

        # Test the agent
        test_dqn_agent()
    

After training the agent for over 50,000 episodes, we reached an incredible milestone: we built an agent that can balance the pole indefinitely. The agent has learned to such an extent that it never lets the pole fall, effectively allowing the game to run forever.

This remarkable result demonstrates the true power of DQN in mastering complex tasks. The agent’s ability to generalize from its training experiences means it has developed an almost flawless understanding of how to keep the pole balanced, regardless of the state it encounters.

While reaching this level of mastery required extensive training and computational resources, it showcases how reinforcement learning can achieve near-perfect performance in environments where traditional algorithms would struggle.

This achievement also highlights an important point: with enough training and the right approach, reinforcement learning can produce agents capable of performing at or beyond human levels, adapting to complex and dynamic environments with ease.

In this article, we’ve seen how DQN overcomes the limitations of Q-Learning by using neural networks, experience replay, and target networks to handle more complex environments. With enough training, we demonstrated that DQN could create an agent capable of mastering the CartPole task indefinitely, showcasing the incredible potential of reinforcement learning.

While DQN is a powerful algorithm, it’s just the beginning. In future articles, we’ll explore more advanced variations like Double DQN and Dueling DQN, which further enhance the agent’s learning abilities.

By applying DQN to CartPole, you’ve taken your first step into the world of deep reinforcement learning. Keep experimenting, and soon you’ll be able to tackle even more challenging environments!